Computer Vision (AI3619)
线性代数知识补充
- 【引理1】 对于二次型
,当 是 的最小特征值 对应的特征向量时,二次型取最小值。如果 是单位向量,则最小值等于 。最大值亦然。由于 是半正定矩阵, 。
CV 中的矩阵求解通常有两种形式:
,利用伪逆求解得到 ,其中 ,本质是最小化 (最小二乘法),根据 【引理1】, 取 对应的特征向量。
成像原理
物体和相机镜头的距离称为深度(depth)
消失点坐标计算:
- 设空间中一组平行线的方向向量为
,则其在图像平面上的消失点坐标为
- 设空间中一组平行线的方向向量为
景深(Depth of Field, DoF):在聚焦的物体前后,被认为清晰的距离范围。i.e., Range of object distances (𝑜 − 𝑜′) over which the image is “sufficiently well” focused. i.e., Range (𝑜 − 𝑜′) for which blur 𝑏 is less than pixel size.
模糊圈直径
与透镜直径 成正比,景深与光圈直径 成反比,与 成反比 暗角:边缘能穿过多个凸透镜的光更少,亮度更低
色差:不同波长的光折射率不同
畸变:镜头缺陷
特征检测
特征的特点:repeatability, saliency(显著性), compactness and efficiency, locality(能表示一块局部区域,对干扰鲁棒性强)
满足上述条件的特征点:团状区域(Blobs as Interest Points)
边缘检测模块:
- 求导检测,在离散的图像中通过差分检测
- 元素之和为0(一阶和二阶都是)
- 小模块定位准,大模块对噪声鲁棒性强
高斯滤波器:
- 用于去噪,也可以写成卷积形式,因此可以和求差分写成一个算子,一阶算子称为
Derivative of Gaussian,二阶算子称为 Laplacian
of Gaussian,表示为
或 - 高斯滤波器对应极值点出现的
称为本征尺度(the 𝜎 at which 2nd Derivative attains its extreme value),它和块的大小成正比 - 为了使对应极值是全局极值(在所有
中也是最大),可以在 Laplacian 上乘一个 (归一化),避免 Laplacian response 随着 增大而减小 越大,图像越模糊
- 用于去噪,也可以写成卷积形式,因此可以和求差分写成一个算子,一阶算子称为
Derivative of Gaussian,二阶算子称为 Laplacian
of Gaussian,表示为
用不同
的高斯对图像做卷积,构成尺度空间(Scale Space) Scale-invariant Feature Transform (SIFT):通过数学建模找出 interesting points 的方法
- 方向匹配:选出八个方向中梯度最大的一个作为主方向,通过减小主方向夹角进行匹配
- SIFT Descriptor: Invariant to Scale, Lighting, Brightness
图像变换
 前者是值域变换,后者是定义域变换
前者是值域变换,后者是定义域变换两个齐次坐标(homogeneous coordinates)(通常写成三元组
)表示同一点,当且仅当其中一个齐次坐标可由另一个齐次坐标乘上一相同非零常数得取得。齐次坐标的相等用 表示。 表示无穷远点。原点表示为 - Any transformation with last row [ 0 0 1 ] we call an affine transformation (仿射变换)
- Any transformation with last row [ g h 1 ] we call an projective transformation, or homography(射影变换)
照片存在射影变换关系的情况:
- 从不同角度拍平面
- 相机沿固定轴心旋转拍非平面
注意各种几何变换的自由度 DOF

射影变换一张图像:对离散的目标像素点求逆变换,在原图像上计算插值(例如 bilinear),保证每个目标点都能被映射到
RANSAC(Random Sample Consensus⭐):随机选一对匹配(s samples),对 inliers 计数,选 inliers 最多的模型
相机标定 Camera Calibration and Photogrammetry
3D to 2D
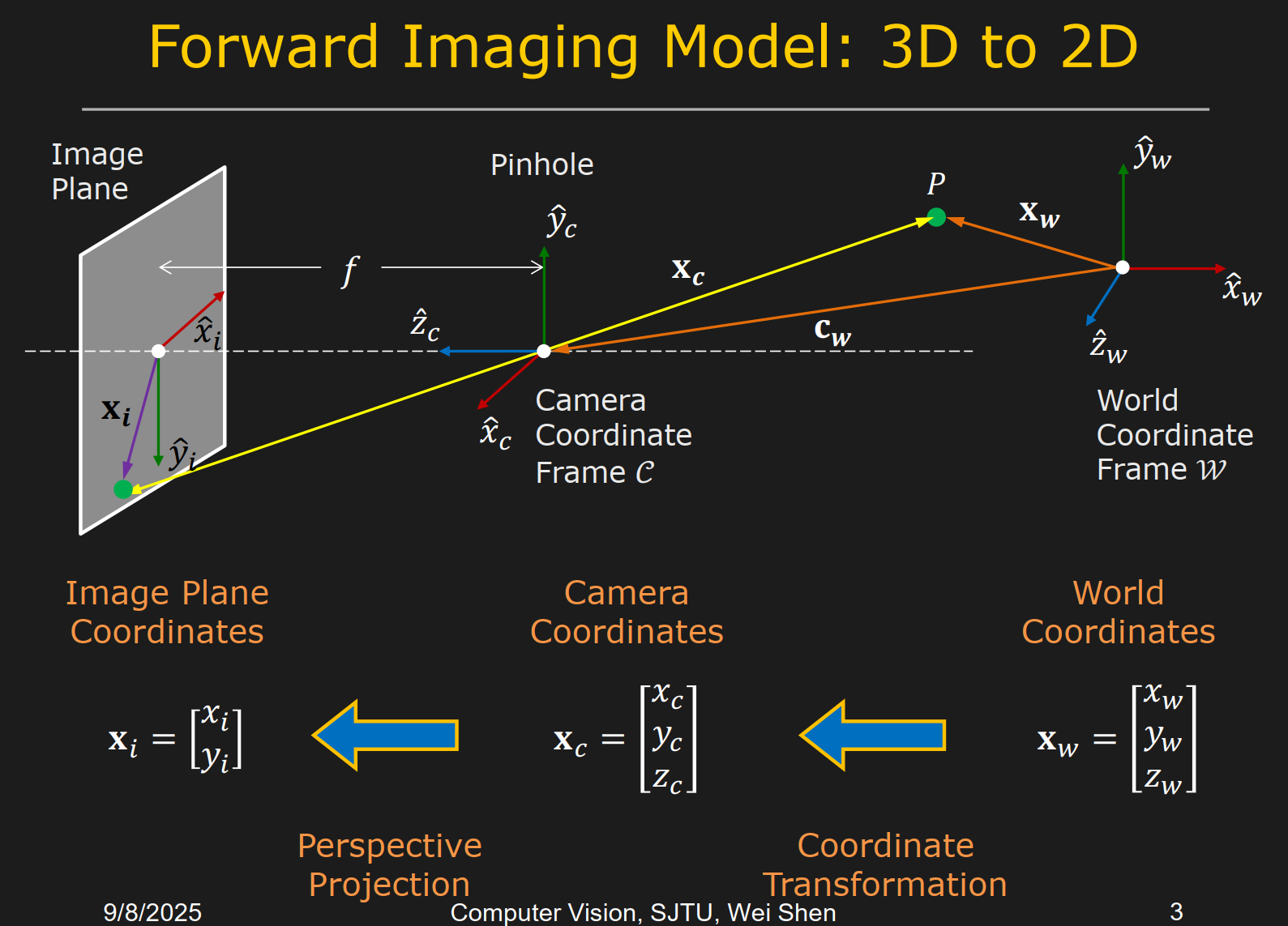
⭐⭐⭐成像公式:
内参矩阵 Intrinsic Matrix:
那么从相机坐标系到图像坐标系的转换可以写为
外参矩阵 Extrinsic Matrix:
其中
综合内外参,相机投影矩阵 Camera Projection Matrix:
于是有
角点检测
考察像素变化
其 中 ( 对 应 梯 度 平 方 ) 是 实 对 称 矩 阵 根据 【引理1】,角点对应的矩阵
联立方程,通过类似方法求出
棋盘格标定(11个未知参数)需要至少3张照片,每张4个角点,其中每张图提供2个独立方程
平行双目视觉⭐⭐⭐
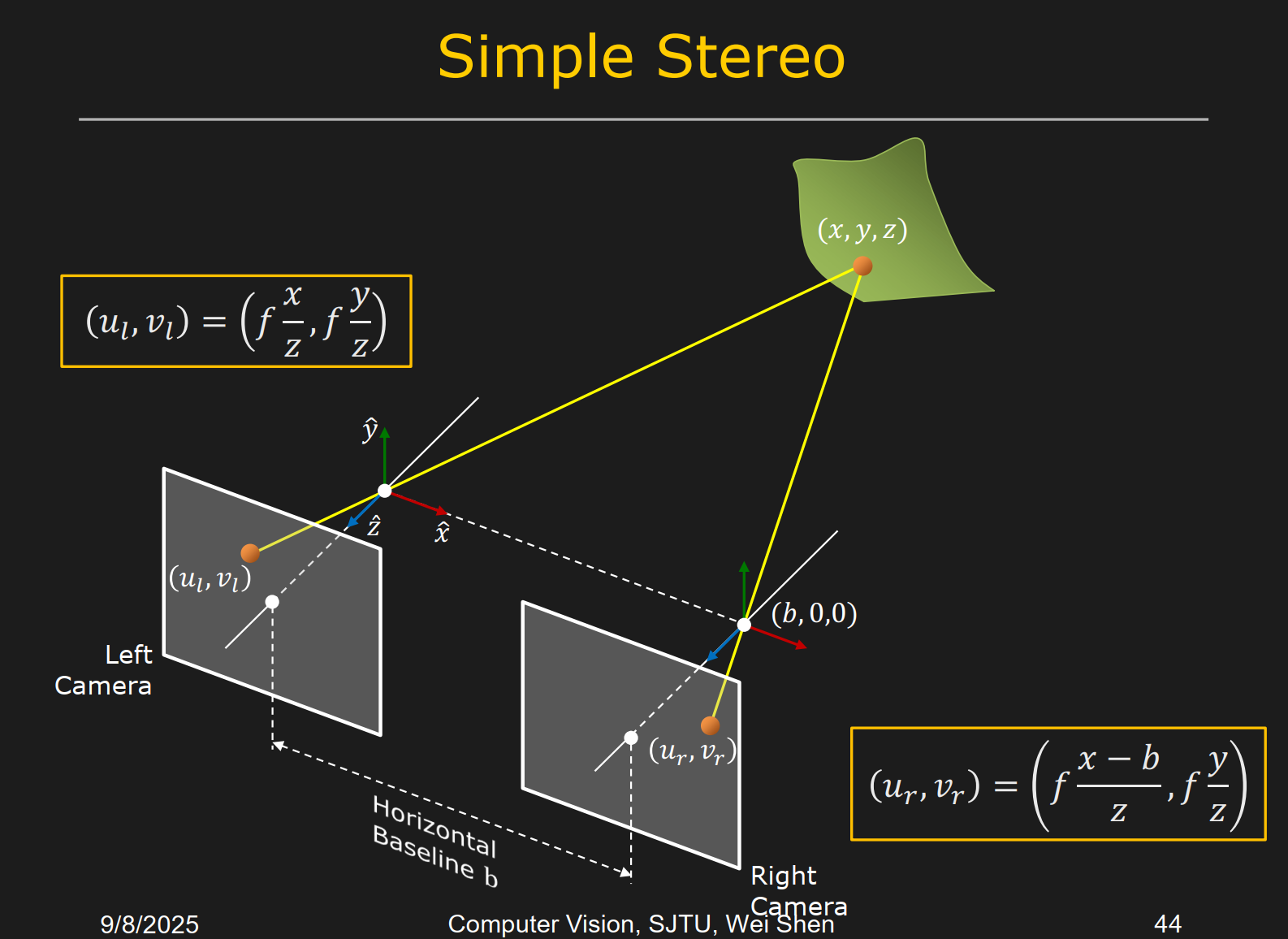
视差(disparity)
深度
立体匹配(stereo matching):在左右图像中找到对应点
- 基于特征的方法:SIFT, Harris corners
- 基于区域的方法(preferred,特征不是每个点都有):SSD, SAD, NCC
立体双目视觉 Binocular Stereo
- 两相机光轴相交时视场比平行时更小
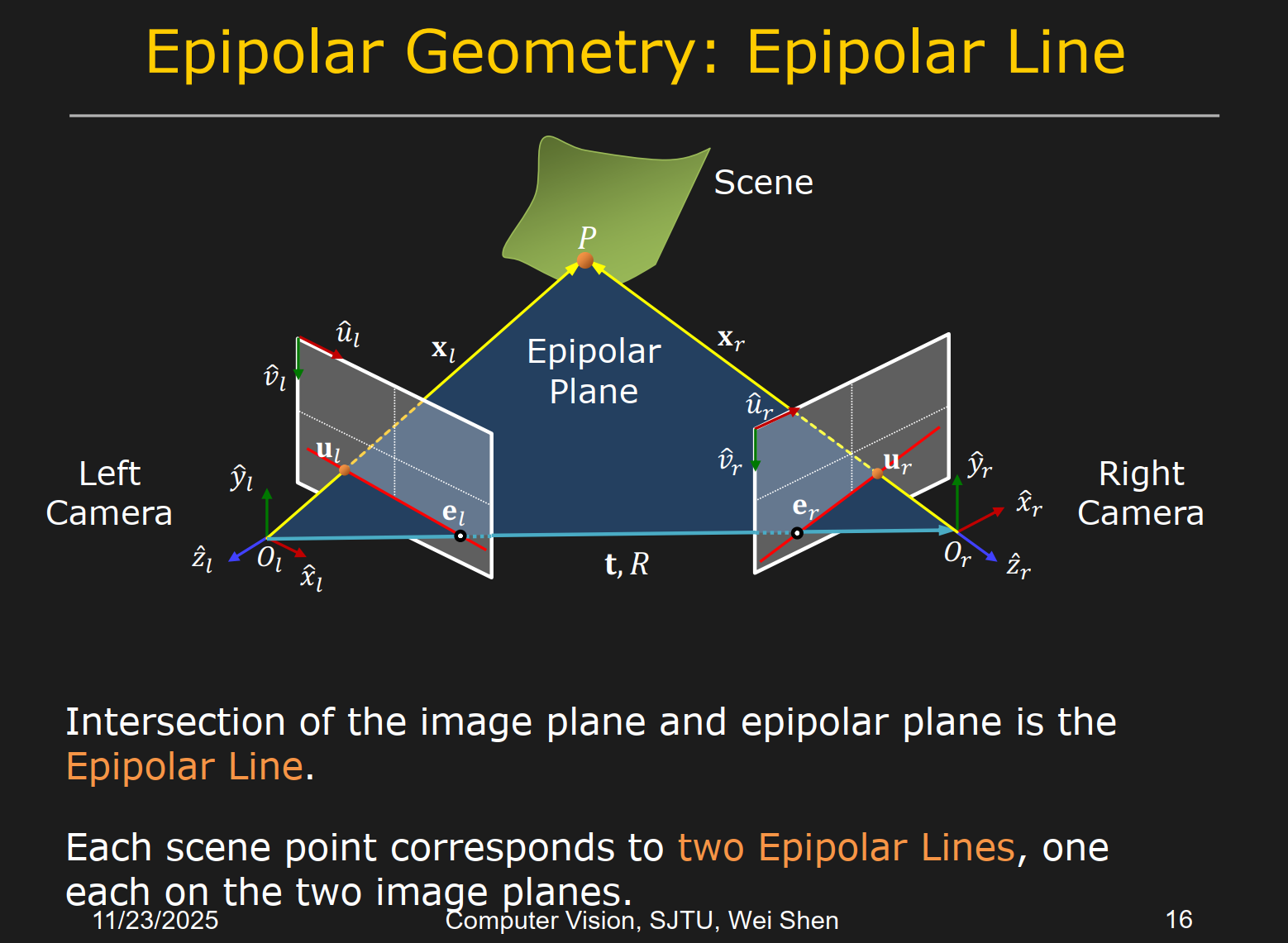
- 本征矩阵 Essential Matrix
基础矩阵 Fundamental Matrix
由
三角测量 Triangulation:四个方程求三个未知数(注意归一化)

关于立体矫正与三角测量 from Gemini
运动光流 Motion & Optical Flow
基本假设:
- 亮度一致(Brightness Constancy):同一物体点在不同帧的亮度不变
- 微小运动(Small Motion):相邻帧之间的位移较小
- 空间一致性(Spatial Coherence):相邻像素点的运动是相似的
光流方程(Optical Flow Equation):
Lucas-Kanade 方法:在一个小窗口内假设光流
视觉识别
构建视觉词典(codebook, or visual vocabulary)的方法:
- 提取特征描述子(如 SIFT)
- 使用聚类算法(如 K-means)对描述子进行聚类,聚类中心作为视觉词典中的“词”
大规模图像检索优化方法:
- 词频-逆文档频率(TF-IDF)加权:提高稀有视觉词的权重,降低常见视觉词的权重
- Inverted file
index:为每个视觉词建立一个倒排索引,记录包含该词的图像列表,提高检索效率
1
2
3视觉词1: 图像A, 图像C
视觉词2: 图像B, 图像C, 图像D
...
图像分割
基于 Bottom-up
层次聚类(Hierarchical Clustering):将视觉词按相似性进行层次化组织,形成树状结构,便于快速检索和匹配
Normalized Cuts (⭐):图像分割方法,将图像表示为图结构,通过最小化切割代价实现分割:
其中
- 构造矩阵
- 构造归一化图拉普拉斯矩阵
- 寻找第二小的特征向量(最小的特征值对应一个 trivial
solution,表示将所有节点放在同一类)
- 对 (y) 进行阈值化以得到聚类
- 理想情况下,通过扫描阈值以获得最小的 N-cut 值
- 构造矩阵
像素之间的权重可以定义为:
基于 Top-down (DL)
评估方法:
Pixel Accuracy:正确分类的像素数占总像素数的比例
⭐Mean Intersection over Union (mIoU):每个类别的交并比的平均值:
其中
Dice loss:衡量预测分割与真实分割之间的相似度:
FCN 利用图像分类方法做图像分割的关键步骤:将 FC 层替换为 1×1 的卷积层(相当于内积),进而保留空间位置信息
可学习的上采样:
- 反卷积(Transposed Convolution):通过插入零值扩展特征图,然后应用卷积核进行卷积操作,实现上采样
目标检测
- 评估指标:IoU, mAP
- Fast R-CNN:使用选择性搜索(Selective Search)生成候选区域(Region Proposals),然后对每个候选区域进行分类和边界框回归
- Faster R-CNN:引入区域建议网络(Region Proposal Network, RPN),实现端到端的目标检测
- RoI feature extraction:通过 RoI Pooling 或 RoI Align 从特征图中提取固定大小的区域特征
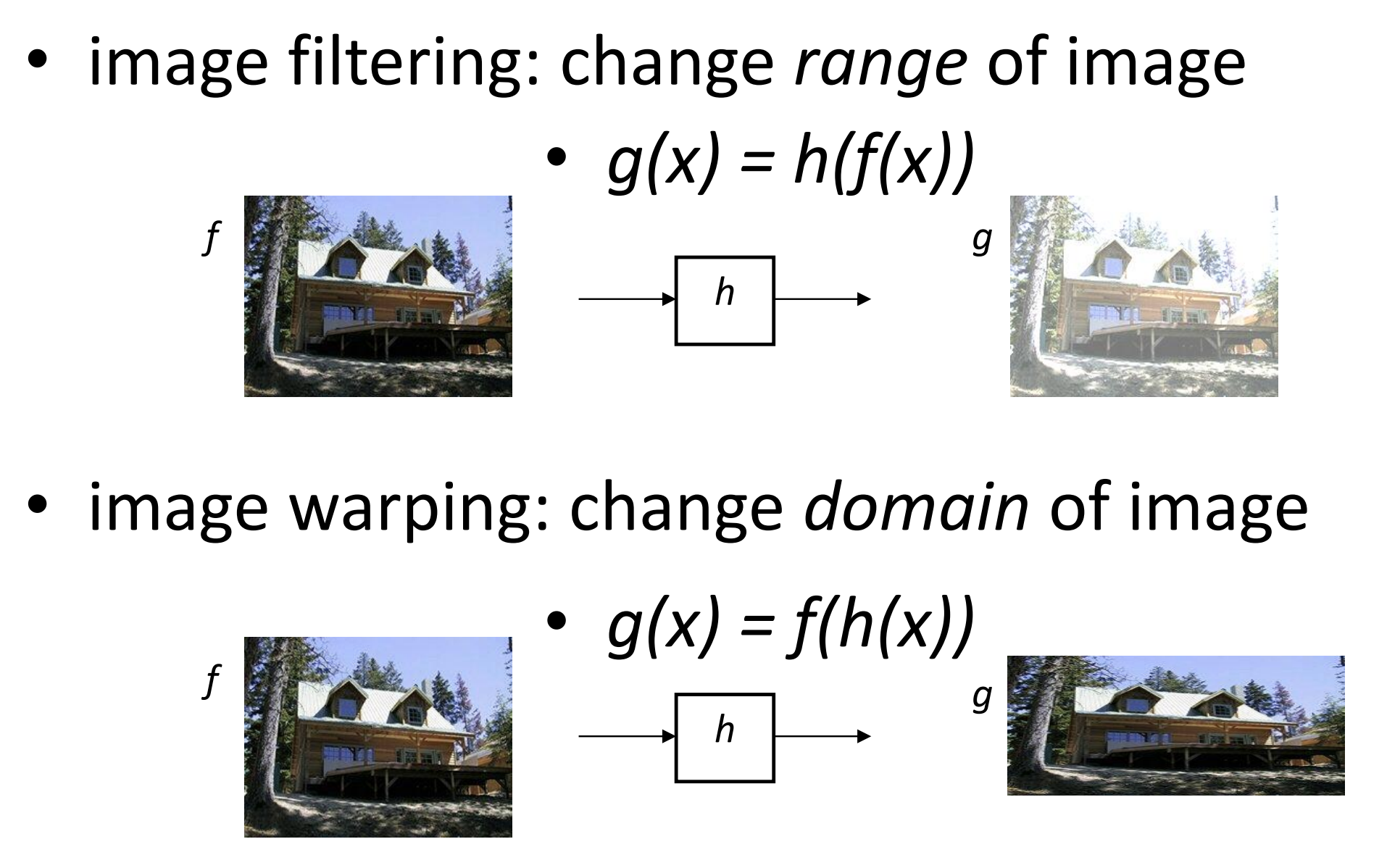 前者是值域变换,后者是定义域变换
前者是值域变换,后者是定义域变换