线性代数的几何本质

线性代数的几何本质

Aronkk
  2025-02-23 2025-02-23 创建   2025-07-13 15:22:50 2025-07-13 15:22:50 更新      730 字  

⚠️ 关于部分设备打开链接显示“视频不见了”的问题：选中网址栏原地复制粘贴回车即可。目前只发现此系列视频有这个问题

学习线性代数的本质后建立的几何直觉

以下结论均基于二维或三维向量，省略了教科书上的标准代数定义，旨在建立可视化的几何直觉(visual geometric intuitions)

设为一个线性变换矩阵，我们有：

  1. 线性变换 保持网格线平行且等距分布，并保持原点不动。常见线性变换有剪切(sheer)，e.g. ；旋转(rotation)，e.g.

  2. 的行列式(determinant) 表示面积或体积的有向缩放比例，行列式为零时发生降维，所降到的维数取决于秩(rank)

  3. 线性方程组 的求解：找到经变换 后变成 的向量

  4. 只要不降维就存在逆变换(inverse)

  5. 的列表示基向量(basis) 变换后的位置

  6. 经变换 后落到原点的向量组成零空间(null space or kernel)

  7. 点积(dot product) 代数与几何定义之间的联系来自于对偶性，详见11分16秒

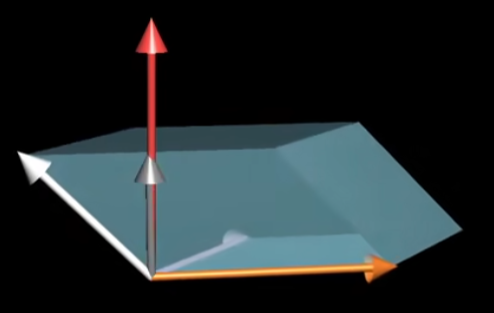
  8. 两个向量叉积(cross product) 数值上等于向量张成的平行四边形有向面积

  9. 经变换 后方向不变的向量 为 的特征向量(eigenvector)， 的缩放比例为特征值(eigenvalue)

    • 对于三维定轴旋转变换，旋转轴上的向量为特征向量，特征值为1
    • 结合第6点，
    • 对于二维旋转变换 ，其特征多项式为 ，它有特征向量和特征值吗？读者不妨细品。

  10. 为正交矩阵等价于线性变换保持长度和夹角不变（仅旋转）

  11. 线性空间：Abstractness is the price of generality（普适的代价是抽象）

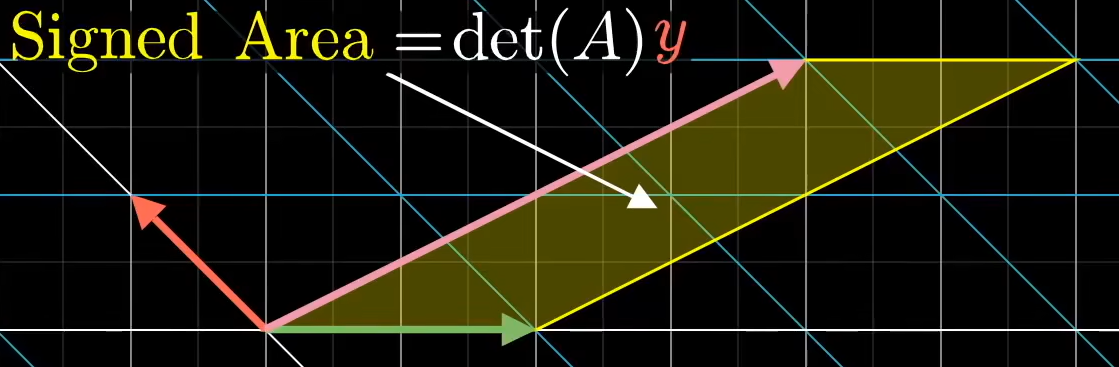
  12. Cramer’s rule: 对于线性方程组 ，

    • 等于 与单位正交基（除去第 个基向量）张成的有向平行四边形面积或平行六面体体积
    • 变换后面积或体积等于 ，其中 表示将 的第 列换成
    • 等于缩放比例 Cramer’s rule 则有

  13. 奇异值分解(Singular Value Decomposition, SVD)：，其中：

    • ：左奇异向量组成的正交矩阵
    • ：对角矩阵，主对角线上是非负的奇异值（从大到小排序）
    • ：右奇异向量组成的正交矩阵的转置

    任何非方阵都可以表示不同维度空间之间的线性变换，SVD 就是将这一变换分解为三个过程（详见 SVD Visualized, Singular Value Decomposition explained | SEE Matrix , Chapter 3）：

    1. 把右奇异向量（由 定义）旋转到标准正交基，例如拥有最大奇异值的奇异向量落在 轴，以此类推
    2. 擦除/添加维度，并在各坐标轴方向上按奇异值拉伸/压缩
    3. 旋转标准基与左奇异向量（由 定义）对齐
目录
线性代数的几何本质
  1. 1. 学习线性代数的本质后建立的几何直觉